Untitled

Mathematics

These are my notes on mathematics. These notes originated as I was trying to recover my lost (or rusty) maths knowledge so I could apply it to game development and building a better understanding of how 3D spaces work.

Pythagoras' Theorem

This is a foundation of geometry, dealing with the relationship between the sides of a right-angle triangle.

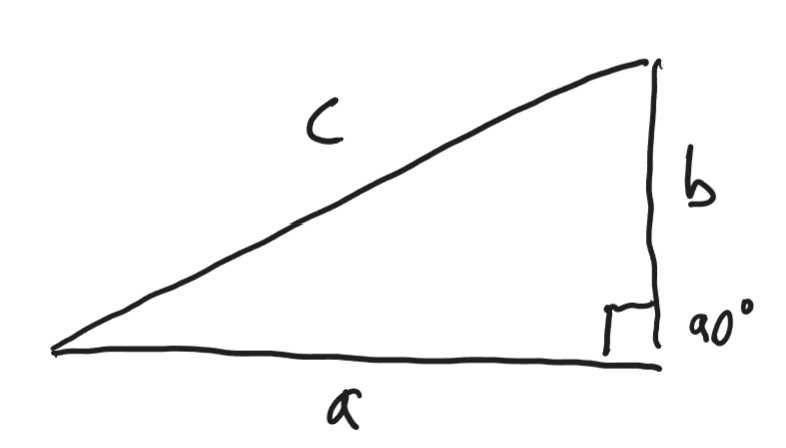
In this triangle, we express the sidea as a, b, and c. We find that the square of a added to the square of b equals the square of c.

We can rearrange this formula as:

Understanding the length of c is useful to us, as typically in a 2D, tile-based space, we can easily discover the X,Y coordinates of objects.

So, as an example:

import math

def distance_between_objects(p1x, p1y, p2y, p2y):
    """
    This calculates the distance between two points in a 2D space.
    """

    distance_x = p1x - p2x
    distance_y = p1y - p2y

    return math.sqrt(distance_x**2 + distance_y**2)

Vectors

A vector is a representation of a direction in a system. Consider the following:

In this system, we assume that a vector is a description of a point in relation to the origin at 0,0. The point is both a description of it's position in space, and the direction relative to the origin.

We describe vectors in a standard way; with a small arrow above the variable name, and listing it's paramaters in a vertical column:

But how do we calculate the length of the vector? It's back to Pythagoras' theorem:

• In this example, we know our coordinate system is orthogonal, so we have a right angle.
• We also know the X and Y position of the point.
• So from there, we can derive the distance from the origin.

You'll notice that we introduce a new piece of notation here. The vector with two vertical bars on either side is to represent the length or magnitude of the vector (the terms are interchangable):

TODO: Adding vectors, 7:32, https://www.youtube.com/watch?v=DPfxjQ6sqrc&t=154s